図51.Photon Wavelength

Photon Wavelength
EWT
●Background
The photon is the carrier of the electromagnetic wave, which is responsible for light, radio waves, microwaves, X-rays, etc.
All of these types of waves are based on the same electromagnetic wave but are differentiated by their wavelengths. Photon wavelength has an inverse relationship to photon energy. For example:
https://energywavetheory.com/photons/photon-wavelengths/
XⅡ 波と確率 より
波動関数とシュレーディンガー方程式
量子物理学における確率の役割については、これまでにも何度か触れてきた。たとえば、電子は原子内のさまざまな場所にそれぞれの確率で見つかる可能性があるとか、二重スリットを抜けた光子がさまざまな場所に、やはりある確率で着地する可能性があるとか、そういった話である。この確率を支配しているものを「波動関数」という。
波動関数によって求められるのが、波の「振幅」だ。振幅とは、波がゼロの値から正または負の方向にどれだけ逃れているかということだ。これはちょうど、水の波が伝わっていくときに、波がないときの水位からどれだけ変化して、高くなったり低くなったりするかというのと似ている。ただし、量子の波と水の波とでは、大きな違いがひとつある。量子的な波そのものは、測定可能な量ではないのだ。測定できる量は確率であって、それは量子波の振幅の2乗である。さらに言うと、量子的な波の振幅は、実数部と虚数部を持った「複素数」になる場合がある。したがって確率は、振幅の「絶対値の2乗」となり、これはたしかに実数なので、測定可能な量である。このあとの話では、専門的な詳細には立ち入らない。とにかく振幅の2乗が確率になる、ということだけ覚えておいてもらいたい。
確率が絡むということは、不確かさがあるということ、つまり確実な知識が得られないということだ。実際、不確定性や「あいまいさ」は、量子物理学のしるしのようなものである。とはいえ、明確なことが何もないわけでもない。ある特定の運動状態にある水素原子内電子の波動案数は、どの点においてもはっきり確定した値をもっている。その2乗である確率も、やはりはっきり確定する。この確定性は、1個の原子から別の原子へと拡張される。1000個の水素原子がすべて同じ運動状態にあったとすれば、それらはすべて同一の波動関数を持ち、同一の確率分布を持つ。確定性がないのは、電子の所在をつきとめるための実験を行なったときに、電子が粒子としてどこに見つかるかという知識である。同一の実験が1000回行なわれれば、電子の所在地は1000回とも違った点になってなっているかもしれない。これは2個の(公正で比重に偏りのない)サイコロを同時に振るようなもので、出た目の和がある特定の数になる確率なら正確にわかるが(和が7なら6分の1、1のぞろ目なら36分の1)、実際にどの目が出るかを事前に知ることは決してできない。
ド・ブロイが物質の波動性を仮定してから1年余りが経った1825年、オーストリアの多才な物理学者、エルヴィン・シュレーディンガーが、いまでも彼の名を冠して呼ばれているひとつの方程式を思いついた。それは波動関数の計算を可能にする方程式で、水素原子に的確に当てはまるだけでなく、原理的にはどんな系にも使えるものだった。シュレーディンガーは当時38歳で、量子力学という新分野のほかの立役者たちに比べれば「年寄り」だった。
シュレーディンガー方程式がなしとげたのは、運動量と波長を結びつけるド・ブロイの考えを一般化することだった。粒子の運動量、ひいては粒子の波長が、ある場所から別の場所へと連続的に変化する状況に広く適用できるようになったのである。一見すると、波が場所ごとに少しずつ異なる波長を持つなどということはありえないように思えるかもしれない。波長はその本質からして、広がりを持つように見える。水の波でも、振動する弦や気柱でも、波長というのは、ある山から次の山までの距離のことなのだ。しかし実際のところ、微小な距離の波長は波の「曲がり」によって定義することができる。図51(画像参照)に示されているように、短い波長を持った波は曲がりが大きく、長い波長を持った波は曲がりが小さい。波長と運動量の反比例関係を覚えているなら、これは粒子の運動量が大きいところでは、粒子が曲がりの大きい波動関数を持ち、運動量の小さいところでは、曲がりの小さい波動関数を持つことを意味している。
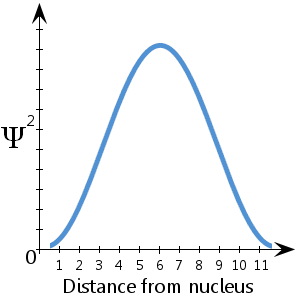
波が円軌道の外周に沿うというド・ブロイのもともとの考えには、それなりの長所があった。そう考えれば、円軌道をとる電子の速さと運動量は一定であるからだ――地球のまわりを回っている衛星と同じである。したがって一定の運動量を持つ電子は、一定の波長を持つことができる。だが、原子核のまわりの円軌道上にいるのではなく、原子核との間を半径方向に行き来する電子はどうなのだろう。電子は原子核に引き寄せられるににつれ、速さを増し、運動量を得る。したがって、その波長は――たとえば原子核から遠く離れたところから、原子核のすぐ近くまで運動するときに――連続的に短くなっていく。ここに登場するのがシュレーディンガー方程式だ。この方程式はその種の運動、すなわち、角運動量がゼロの運動を解を与える。それを特定の基底状態の場合であらわしたのが図52(画像参照)だ。原子核に近いところでは波動関数が大きく曲がり、原子核から遠いところでは波動関数の曲がりが小さくなっている。
図52には、波動関数に関するもう2つのポイントが描かれている。第1に、グラフは小さい値から上昇して大きい値になり、また小さい値に戻っており、これは原子の片側からもう片側もでの1サイクルの振動の半分を示している。ということは、このグラフはほぼ平均の波長をあらわしていて、それはおよそ0.2ナノメートル(2x10-10メートル)である。そしてそこから、この状態にある電子のほぼ平均の運動量がわかるのである。第2に、電子に波動性があるために、円周方向にであれ半径方向にであれ、単純な軌跡はたどれない。電子の波はつねに広がっていくのだ。図52のグラフに描かれている特定の運動量だと、中心から外向きのすべての方向でまったく同じように見えるファジーなボールを考えなければならない。電子の波動関数はボールの外側のまわりでは小さな値を持ち、ボールの中心に向かって動くにつれて大きな値になっていく。それに関しては、どの方向もまったく同じである。