ゆっくり解説】ミクロな世界の理論的限界-プランクの長さ-
Rayleigh-Jeans vs Planck
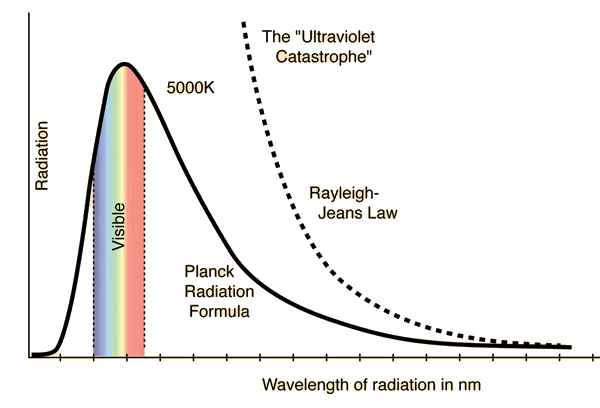
Comparison of the classical Rayleigh-Jeans Law and the quantum Planck radiation formula. Experiment confirms the Planck relationship.
Blackbody Radiation
"Blackbody radiation" or "cavity radiation" refers to an object or system which absorbs all radiation incident upon it and re-radiates energy which is characteristic of this radiating system only, not dependent upon the type of radiation which is incident upon it. The radiated energy can be considered to be produced by standing wave or resonant modes of the cavity which is radiating.
http://hyperphysics.phy-astr.gsu.edu/hbase/mod6.html
Ⅱ 原子核の奥へ より
プランク定数とは何ですか
ベルリン大学の教授だったマックス・プランクは、1900年に、量子時代の幕開けを告げる発見をした(自分がひとつの革命の火ぶたを切って落としたとは思いもよらずに)。当時のプランクが悩まされていたのは、いわゆる「空洞放射」についてで、まずはこれを説明しておこう。
この年、古典物理学は全盛を極め、力学と熱力学と電磁気学のすばらしい理論によって物理世界がこんなにも理解できるのだということで、当然ながら物理学者は、たいへんいい気分に浸っていた(うぬぼれてさえいた、とあえて言わせていただこう)。たしかに古典物理学の堂々たる体系には、いくつか小さなひびもある。しかし、古典物理学それ自体を使って、それらのひびも修復できるだろうと大半の物理学者は思っていた。たとえば、なぜ原子がそれぞれ特定の振動数の光を放っているのかは誰も知らなかった。そのころ発見されたばかりの放射性物質のふるまいについても、誰も理解していなかった。この2つの問題にどう取り組めばいいか誰もわからなかったから、いずれ古典物理学を使ってこれらを説明できるだろうと考えた(もしくは単に期待した)としても無理はなかった。だが、物理学の体系にはもうひとつ難点があって、こちらはさらに悩ましかった。というのも、それは説明できて当然の問題だったのだ。これが空洞放射の謎である。
あらゆるものは放射を発する。そしてその強度と振動数の分布は、放射を発するものの温度に依存する。太陽や焚き火の場合、その放射は容易に目に見える。温まりはじめたばかりの電気ヒーターの場合は、赤色発光がかろうじて見える。そしてあなたの寝室の壁の場合、放射はまったく目に見えない。なぜならその放射は弱く、しかも振動数は赤外線域にあるからだ。とはいえ、それは昼間の太陽光と同じように確実に存在している。そこで、この寝室えお大きな箱に置き換え、その箱の壁をある一定の温度に保たせたとしよう。壁は内部に向かって絶え間なく放射を発すると同時に、絶え間なく放射を吸収する。この箱――すなわち空洞――の内部では、さまざまな振動数の電磁波があちこちに行き交じっている。プランクの研究以前に科学者がわかっていたのは、空洞ないの放射が壁の温度だけによって決まるのであり、壁の組成や空洞が壁の大きさは関係しないということだった。この空洞放射の強度が振動数ごとにどのように変化するかを示したのが図(画像参照)である。
プランクの研究が登場するまで、図に描かれている温度分布を説明しようとする試みはすべて失敗に終わっていた。古典的な理論では、空洞内での放射の強度が無限になるというばかげた予測までされてしまった。1900年の晩秋、さまざまな試みが繰り返されたすえに、当時42歳のプランクがついに空洞放射の説明に成功した――が、そこにいたるためには、プランク自身が言うところの「やけっぱちの行為」が必要だった。プランクは、空洞の壁にある「共鳴子」(特定の振動数で振動する電荷)が放射を束としてだけ放出したり吸収したりするのだと仮定して、その束を「量子」と称した。そして彼の理論では、それぞれの束――それぞれの量子――は振動数に正比例するエネルギーを持っていた。プランクはそれを次のような方程式であらわした。
E = hf
Eは共鳴子から発せられる量子化されたエネルギーの束で、fは発せられた放射の振動数(たとえば1秒あたりの振動数なら、単位はヘルツ)、hはプランクが導入した新しい定数である。高い振動数の量子は、低い振動数の量子より大きなエネルギーを持つ。プランクは自分の導入した新しい定数を示すのにhの文字を使ったが、誰もそれを変えようとしなかったので、そのままhで定着した。もうお察しだろうが、このhが、現在知られているプランク定数である。空洞放射についてのデータから、プランクは十分に正確なhの値を計算することができた。日常的なエネルギーの単位ジュールと振動数の単位ヘルツであらわすと、hの値はとてつもなく小さく、10-33より小さい。
プランク定数は、物理学におけるまったく新しい考えの誕生を告げるものだった。
わたしたちの身のまわりの世界における運動や変化は、古典物理学で考えられていたほどなめらかで連続的ではなく、むしろざらざらした「塊」でできているようなものだという考えである。さらに、プランク定数のとてつもない数値の小ささは、微小な量子世界のスケールを確立した。仮に、プランク定数のhの値が、この世界における値よりずっと大きい世界があったなら、そこでは量子効果が大きく、ひとめでそれとわかるだろう。あるいは逆に、hの値がこの世界における値よりずっと小さい世界があったらどうだろう。そこでは量子効果がさらに狭い範囲に押し込められて、日常世界からさらにかけ離れたものとなるだろう。そしてはたまた、hの値が奇跡的にもゼロにまで下がっている世界があったなら、そこには量子効果のない、純粋に古典的な世界であり、このような本が必要とされることもないだろう(そして、空洞放射があらゆるものをこんがり焼きあげる世界でもある)。
最後にひとつ、プランク定数に関する追記をしておこう。20世紀初期に量子物理学が発達すると、物理学者は自分の記述する方程式にたびたびhが2πで割られるかたちで出てくることに気づくこととなった。たとえば、原子内の電子の軌道運動の強さ(すなわち電子の「軌道角運動量」)はh/2π、または2(h/2π)、3(h/2π)、……などと等しい値になっていたのである。そこで物理学者は略記として、h/2πをħ(hの縦線に短いバーをクロスさせたもの)と表記して、「エイチ・バー」と呼ぶようになった。