Schrodinger equation
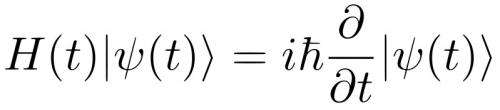
The Beginnings and Evolution of Algebra
『数学のすべてがわかる本』
科学雑学研究倶楽部/編 学研プラス 2018年発行
3次元方程式で注目された虚数の発見 より
実在しない数!? 虚数とは
カルダーノの問題『偉大なる術』が虚数の始まりだといわれたことは述べてきました。では、虚数とは、どのようなものでしょうか。
簡単にいえば2乗したときマイナスになる数のことです。考えてもらうとわかると思いますが、同じ数字どうしでかければ、必ずプラスの数になるので、虚数は実際にはない数字です。実際にないのに、なぜそんなものを数字とするのでしょうか?
虚数のルーツを探っていきますと、ピタゴラスの定理になります。
ピタゴラスは、√2という数字に悩みました。たとえば、ピタゴラスの定理の定理では、直角二等辺三角形で、直角を挟む2辺が「1」の場合、斜辺は√2になります。しかし√2は1.41421……と無限に続き、現代では無理数と分類される数字ですが、ピタゴラスはすべての数は整数の比で表されると信じていたので、√2は「存在しない数」だったのです。数としては存在しないけれど、図形では直角を挟む2辺が「1」の直角二等辺三角形が存在するのです。
虚数は人類が生み出した知恵?
カルダーノは、『偉大なる術』の中で、「和が10、積が40になるふたつの数を求めよ」という問題を出しています。これを現代の式で表すと、次のようになります。
x + y = 10 ……①
xy = 40 ……②
①より、 y = -x + 10 ……①'
①'を②へ代入
x(-x + 10) = 40
-x^ + 10x = 40 (^は2乗)
x^ - 10x + 40 = 0
解の公式より、
x = ( 10 ± √(100 - 160) ) / 2
= 5 ± √-15
カルダーノの問題を現代の式で解いたもの。√-15 は虚数である。
「答えがないから、無理やり数字を作った」といえば、何とも安易な方法と思うかもしれませんが、便利な「人類の知恵」と考えることもできそうです。
実際に、中学校で習う2次方程式は、「解がない」ということで終わることがありますが、虚数という概念を使えば、解ができてしまうのですから、やっぱり虚数というのは便利なものといえそうです。
-
-
-
-
-
-
-
-
-
-
-
- -
-
-
-
-
-
-
-
-
-
-
おバカな、じじぃの日記。
虚数・・・実数ではない複素数のことである。ただし、しばしば「虚数」と訳される英語の "imaginary number" は、「2乗した値がゼロを超えない実数になる複素数」として定義される場合がある。iで表される虚数単位は代表的な虚数の例である。
シュレーディンガー方程式・・・物理学の量子力学における基礎方程式である。 シュレーディンガー方程式という名前は、提案者であるオーストリアの物理学者エルヴィン・シュレーディンガーにちなむ。1926年にシュレーディンガーは量子力学の基礎理論に関する一連の論文を提出した。シュレーディンガー方程式の解は一般的に波動関数と呼ばれる。
ぼけっと、『数学のすべてがわかる本』を見ていたら「虚数」というのが出てきた。
「簡単にいえば2乗したときマイナスになる数のことです」 (^^;;
虚数は単位として「i」で表すことが多い。
よく、物理の本には「シュレディンガーの波動方程式」が登場する。
このシュレディンガーの波動方程式の中に虚数「i」が入っているのを初めて気がついた。
虚数を使うことを前提とする量子力学と呼ばれる物理学で、さまざまな現象を説明できるのだという。
来年は、少し虚数を勉強することにした。