Universe model - Aristotle
平行線公理

地球に描く三角形の和は270度
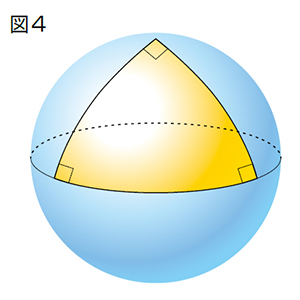
3つの角が直角の三角形
●ユークリッド幾何学と非ユークリッド幾何学
「三角形の内角の和が180°でない三角形がある」など、非ユークリッド幾何学の話を通して、
幾何学に興味をもつことが、この教材のねらいである。
http://www7b.biglobe.ne.jp/~math-tota/suA/euclid.htm
証明 より
前提が違えば三角形の内角の和も180度ではなくなる
公理とは、ある理論の出発点となる大前提のことです。公理という前提がなければ、どんな証明も成り立たないという話です。
事実、ユークリッド幾何学で完璧に証明されている「三角形の内角の和」も、公理が違えば盤石ではありません。というのも、ユークリッド幾何学は「平行線公理」をひとつの前提としています。
「1つの線分が2つの直線に交わり、同じ側の内角の和が2直線より小さいならば、この2つの直線は限りなく延長されると、2直線より小さい角のある側において交わる」
という読んでイヤになる公理ですが、「または」と「かつ」がベン図でわかりやすくなるのと同様、これも図で見ればべつに難しくありません(画像参照.平行線公理)。
・
でも、じつはこの公理が成り立たない世界があります。それは「曲面」です。α+βがぴったり180度のときに2直線がどこまでも平行になるには、そこが「平面」でなければなりません。そのことは、地球儀を見てもらえばすぐにわかります。緯度と経度はどの点でも直角に交わっているので、平面上ならどこまでも平行のはず。しかしすべての緯度と経度は、北極と南極で交わります。
そこでは三角形の内角の和も180度とはかぎりません。1例として、北極で直角に交わる2本の経線とそれに挟まれる赤道で作る巨大な三角形を考えてみてください。赤道(緯度)は経線と直角に交わるので、この三角形の3つの角はすべて90度。したがって内角の和は、90x3 = 270度になるのです(画像参照.地球に描く三角形の和は270度)。こうなると、非ユークリッド幾何学のワールドです。
ユークリッド幾何学の話が長くなってしまいましたが、ここで理解してほしいのは論理的に何かを証明するときには「前提」が大事ということ。感動的なほど厳密で完璧な幾何学の証明でさえ、公理という前提が崩れると簡単にひっくり返ってしまうのです。
ですから、論理的に物事を考えて何らかの結論を導こうとするときは、そもそもの前提におかしなところがないかどうかを確認しなければいけません。曲面の話をしているのに平面の公理を前提にしていたのでは、途中のロジックがどんなに正しくても間違った結論しか出ないでしょう。
-
-
-
-
-
-
-
-
- -
-
-
-
-
-
-
-
どうでもいい、じじぃの日記。
古代ギリシア(紀元前500年頃)の哲学や思想は、現代の我々の「知」の原点として参照され続けている。
現代の原子論とは少し違うが、物質が最小の単位 原子から構成されている、という考え方はデモクリトスによって唱えられた。
アリストテレスは、現代の天文学、生物学、気象学など「万学の祖」とされる。
彼は、地上界は土、水、空気、火の4元素からなるとし、天上界(宇宙)は地球中心の天動説を唱えた。
実際は、自然の物質は原子から構成されており、地球は太陽を中心とした太陽系惑星の1つでしかない。
「ですから、論理的に物事を考えて何らかの結論を導こうとするときは、そもそもの前提におかしなところがないかどうかを確認しなければいけません」
見えているものが、 必ずしも真実とは限らない、ということか。
言うのは簡単だが、私なんかはアリストテレス的な思考に染まって生きているのかもしれない。
トホホのホ。