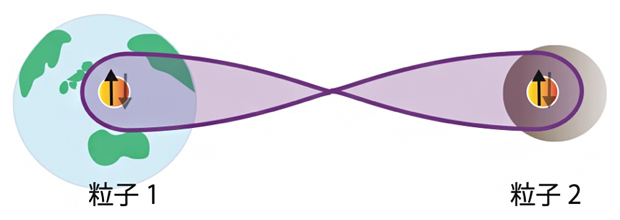
図1 量子もつれのイメージ図
粒子1と粒子2が量子的にもつれた状態にあるとき、互いにどんな離れた場所にあっても、粒子1に対する測定は瞬時に粒子2の測定結果に影響を与える。
量子もつれの境界則に対する新しいメカニズムの発見
2020年9月8日 理化学研究所、慶應義塾大学
例えば、二つの粒子にスピンという自由度がある場合を考えます。スピンは、上向きと下向きを持つ小さな磁石と見なすこともできます。最初に、2個の粒子のスピンに相関のある状態を作り、一つ目の粒子を地球上に、二つ目の粒子を月面に移動させます。量子力学の世界では、粒子間が遠く離れていても有限の相関を持つ状態が存在し得ます。そのため、地球上の粒子のスピンで上向きを観測したとき、月面上の粒子のスピンも必ず上向きになる、あるいは逆に、地球上で下向きを観測したら月面上でも下向きになる、といった古典力学系ではあり得ないような相関を生み出すことができます。
このような性質のことを「量子もつれ(量子エンタングルメント)」といいます(図1)。近年進歩が目覚ましい量子コンピュータを用いた量子計算においては、この量子もつれが重要な役割を果たします。
https://www.riken.jp/press/2020/20200908_2/index.html
XV 量子物理学に残された謎 より
エンタングルメント(量子もつれ)とは何ですか
エンタングルメント(量子もつれ)に関しては、それだけで本が何冊も書けるだろう(実際、書かれている)。基本的な考えは単純だが、わたしたちがこれを信じられるかというと、そのハードルは高い。エンタングルメントはある種の重ね合わせである――ただし重ね合された状態が、普通に量子効果が及ぶ範囲をはるかに超えて、大きな距離に広がっているのである。
あらゆる量子状態は、2つ以上の異なる状態の重ね合わせであらわすことができる。
たとえば項目76(重ね合わせとは何ですか)で述べたように、北向きのスピンを持っている電子は、それと同時に、東向きのスピンと西向きのスピンを持った状態の重ね合わせになっている。基底状態の水素原子内の電子も、それと同時に無数の状態の重ね合わせになっていて、それぞれの状態が電子をある特定の場所に局在化している。このような種類の重ね合わせは、たしかに常識外の考えではあるが、エンタングルメントという種類の重ね合わせほど脳に負担を強いるものではない。
たとえば、電気的に中性のパイ中間子が静止していて、ある時点で崩壊して2個の光子に変わるとしよう。最初のパイ中間子は、電荷がゼロ、運動量もゼロ、角運動量(スピン)もゼロだ。これらは保存される量であるから、崩壊生成物のそれらの値もやはりゼロになる。2個の光子なら、電荷はゼロだ。電荷の保存は守られている。2個の光子は等しい運動量で背中合わせに飛び散っていくので、運動量の保存も守られている。向きが逆になっている2つの等しいベクトル量のベクトル和はゼロであるからだ。そして2個の光子のスパン方向も、当然、全スピン量ゼロを保存するために逆向きになっていなくてはならない。だが、飛び散っていく2個の光子は観測されるまでは単一の系で、向きが逆になっている運動量、向きが逆になっているスピンの重ね合わせになっている。仮に1個の光子が左に飛び去れば、もう1個の光子は右に飛び去る。左に飛び去った光子のスピンで左向きだった場合には、右に飛び去った光子のスピンは右向きでなければならない。この状態は[L、R]と略記される。もしも左に飛び去った光子のスピンが右向きだったら、右に飛び去った光子のスピンは左向きでなくてはならない。この状態は[R、L]とあらわすことができる。実際に崩壊過程で生じている状態は、この2つの(飛んでいく方向ごとに2つの)可能性が等しい割合で混ざりあっている(重ね合わせになっている)。この状態は、[L、R]-[R、L]と書きあらわせる。つまり左に飛び去った光子のスピンの方向を測定したときに、それが左向きとわかるか右向きとわかるかの確率は五分五分だということだ。
ここに、アインシュタインの言う「不気味な遠隔作用」が関わってくる。
あなたが左に飛び去った光子のスピンを、光子の生成されたところから1メートル先のところでも、1キロメートル先のところでも、1光年先のところでも測定できるとしよう。そして測定した瞬間、あなたはもう1個の光子のスピンも特定できている。たとえその光子が2メートル先にいたとしても、2キロ先にいたとしても、2光年先にいたとしてもだ。1個の光子のスピン方向がひとたび確実に確定すれば、たとえ測定がなされるまでは両方の光子のスピン方向が不確定で不明だったとしても、その時点でもう1個の光子のスピン方向が決定されるのである。なぜそうなるかといえば、測定の瞬間までは、2個の光子が1つの量子系を構成しているからだ。2個の光子は2つの別々の系ではないのである。
ドイツからの移民としてアメリカに渡ってきてから2年が経った1935年、アルベルト・アインシュタインは、プリンストン高等研究所での2人の同僚、ボリス・ポドルスキーとネーサン・ローゼンとともに、量子物理学の分野で史上最も有名な論文のひとつを発表した。といっても、その論文の目的は量子物理学に疑問を投げることであって、量子物理学を発展させることではなかったかもしれない。いや、むしろこの論文は、いまわたしが述べたようなことを受け入れられる人間の正気に対して疑問を投げかけている、とさえ言えるかもしれない。ある系の一部が測定された瞬間に、そこから遠く離れたところにある。一見するとまったく無関係な、同じ系の別の一部が、なぜか急にぱっと気をつけの姿勢をとる……そんな主張が受け入れられようか?
いずれにしても、EPR――上記の共著者3人の総称で、彼らは以後ずっとこう呼ばれてきた――が記述したのは、彼らが取り込んでいた以下のような状況である。2つの系が近づきあって、相互作用して、また別れる。量子物理学にしたがえば、この2つの系は相互作用により「エンタングル」した(もつれた)状態(この用語は、EPRの論文が出た直後にエルヴィン・シュレディンガーが導入した)になっており、何らかの測定がなされて「もつれ」が解かれるまで、2つの系は実質的に――どれだけ離れていようと――振幅が重ね合され、それぞれの状態に対する1つの相対確率を持つ系であって、それらが相互作用をした空間領域にそのまま閉じ込められていた場合となんら変わらない。しかしEPRには、別の主張があった。何メートルも何キロメートルも何光年も離れたところで一方の系に測定がなされた瞬間、他方がそれに反応するなどという考えは合理性を欠いており、したがって間違っているに違いない、と見なしたのである。重ね合わせという考え方を、彼らにとっては「不合理」と思われるところまで押し広げることにより、EPRは量子物理学に穴を見つけたと――あるいは少なくとも、物理学者たちによる量子物理学の記述に、穴を見つけたと考えたのだった。
ある場所で行なわれた測定によって、別の場所の何かについての情報がもたらされるという考えは、それ自体としてはさほど奇妙でもない。
・