Traveling Salesman Problem Visualization 動画 YouTube
https://www.youtube.com/watch?v=SC5CX8drAtU
図1-1
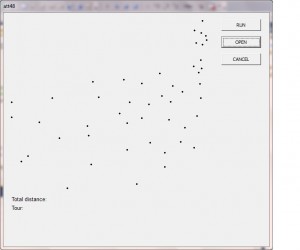
図1-2
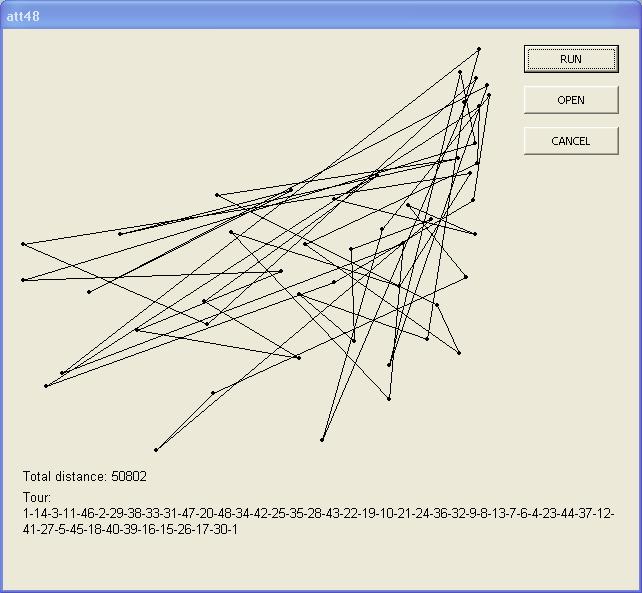
図2

C++ 2-opt Traveling Salesman Problem 2012年4月20日 technical-recipes.com
Some initial results from experimenting with the 2-opt heuristic and applying it to a standard traveling salesman test problem.
http://www.technical-recipes.com/2012/applying-c-implementations-of-2-opt-to-travelling-salesman-problems/
巡回セールスマン問題 ウィキペディア(Wikipedia)より
巡回セールスマン問題(traveling salesman problem、TSP)は、都市の集合と各2都市間の移動コスト(たとえば距離)が与えられたとき、全ての都市をちょうど一度ずつ巡り出発地に戻る巡回路の総移動コストが最小のものを求める(セールスマンが所定の複数の都市を1回だけ巡回する場合の最短経路を求める)組合せ最適化問題である。
-
-
-
-
-
-
-
-
-
-
-
- -
-
-
-
-
-
-
-
-
-
-
『続 5分でたのしむ数学50話』 エアハルト・ベーレンツ/著、鈴木直/ 岩波書店 2008年発行
巡回セールスマン より
具体的な最適化問題を「散歩」にたとえて理解するには、少しばかり慣れが必要だ。そこで1例として正編の第46話でとりあげた巡回セールスマンに助け舟を出してみることにしよう。たとえば20都市が与えられているとして、それを最短距離で巡回するものとしよう。それぞれの都市に1、2、…、20までの番号を振り、巡回ルートを簡単に数列で表わすことにする。たとえば
6、1、19、2、15、12、3、5、20、11、16、10、7、13、8、4、9、17、14、18
という数列は、都市6から出発し、都市1に向かい、そこから都市19へ行き、…という道順を示している(そして20番目の目的地、つまり都市18に着いたら、ふたたび都市6に戻る)。
こういう巡回ルートの総数は天文学的数字になる。基本的な組合せ理論によれば全部で243京2902兆81億7664万通りの可能性がある。このすべての巡回ルートについてその全長をコンピュータで計算しようとするのは現実離れしている。しかし、すべての巡回ルートを、先の例でいえばある土地の中の位置と考え、現在のルートの全長をその土地の海抜と考えることができる。そのうえで1番低い地点を探しだす。
シミュレーティド・アニーリング(焼きなまし法)を使うとすれば、以下のような手順で解を探すことになるだろう。まず、何か具体的なルート、たとえば上に上げた例(6、1、19、…)から作業を開始する。まずここで巡回ルートの中から任意の2都市を適当に選び出し、それを入れ替える。たとえば今、その2都市として3番目に訪れる都市と8番目に訪れる都市が偶然に選ばれたとしよう。すると上の数列は以下のように変わる。
6、1、5、2、15、12、3、19、20、11、16、10、7、13、8、4、9、17、14、18
つまり都市5と都市19が入れ替わったわけだ。もしそれで全長が短縮されたならば、そこを出発点としてさらに同じ作業を反復する。もし短縮されなければ、もとに戻って別の可能性を試してみる。ここで重要なことは、ある一定の確率で、全長がより長くなる巡回ルートも受け入れるということだ。しかもその頻度は最後のほうよりも最初のほうを高くする。こうすることで局所的な最小値を抜け出す(つまり高原の窪地ではなく、ほんとうに11番深い谷を発見する)道を確保する。
以下にシミュレーティド・アニーリングが使用される具体例をあげよう。与えられているのは平面状に存在する20の「都市」だ。それは図1の上に描かれている。ここでは、都市間の距離を点と点を結ぶ直線の長さ――すなわち最短距離――で測ることにしよう(具体的な例ではもっと別の数字、たとえば鉄道路線の長さなどが使われるかもしれない)。ここで、ある偶然によってなんらかのルートが選ばれ、最初の巡回プランが提案される。かなり混沌としたその結果は図1の下に示されている。
そこでアニーリング・アルゴリズムの出番が回ってくる。すでに述べたように、このアルゴリズムは、今まさに提案されていいるルートのヴァリエーションを探し、通常は今より短い道のりになる提案だけを追いかけていく。1000分の数秒の時間があれば、コンピュータは図2のようなルートを発見するだろう。
これはすでに、かなり理にかなったルートに見える。これよりも画期的に短くなるような道はないように思える。
しかし注意すべきは、それでもまださらに巡回距離を節約する方法が絶対ないとは言いきれない点だ。ただし、それを確実に保証しようと思うなら、これより格段に多くの数学理論と計算時間を投資しなければならなくなるだろう。