天才アインシュタインの脳の秘密 2-1 動画 YouTube
http://www.youtube.com/watch?v=L7esjS8PdHE
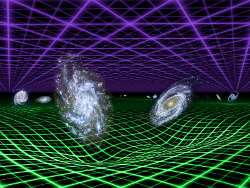
重力場
マルセル・グロスマン ウィキペディア(Wikipedia)より
マルセル・グロスマン(Marcel Grossmann, 1878年4月9日 - 1936年9月7日)は、ハンガリーのブダペスト出身の数学者。
アルベルト・アインシュタインの友人であり同級生として知られる。
彼はチューリッヒにあるチューリッヒ工科大学の数学科画法幾何学専攻の教授となった。一般相対性理論の発展に必用不可欠な方法としてリーマン幾何学の重要性をアインシュタインに説いたのはグロスマンであった。
アブラハム・パイスの著書によればグロスマンはテンソル理論についてアインシュタインに対してよき相談者であった。相対論の研究者達はグロスマンの物理学への貢献を賞賛して、3年ごとに開催される国際会議の名前を「マルセル・グロスマン会議」(Marcel Grossman meetings;略称MG)とした。
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- -
-
-
-
-
-
-
-
-
-
-
-
-
-
『宇宙論大全 相対性理論から、ビッグバン、インフレーション、マルチバースへ』 ジョン・D・バロウ/著、林一、林大/訳 青土社 2013年発行
アインシュタインの洞察 (一部抜粋しています)
アインシュタインの一般相対性理論は、理解不可能なものと難解なものの代名詞になっている。知性にとっての究極の難題だ。確かに、運動と重力についての新たな法則をコペルニクス的に表現するのにアインシュタインが用いた数学の言葉は、本人にとっても初めは手ごわいものだった。自分は数学の能力が足りないとアインシュタインは告白している。アインシュタインの特別な才能は、物理を理解する能力であって、数学の天才的才能ではなかった。だがアインシュタインは、何らかの数学的計算ができなくとも普通、それができる人を知っていた。学生時代からの友人マルセル・グロスマンは才能ある数学者で、現代数学のとりわけ抽象的な分野に通じていた。グロスマンはまた、自然の仕組みの核心を見抜くアインシュタインの目覚ましい才能を認識していて、この人を助けるためなら、できることは何でもしたいと思っていた。1912年アインシュタインはチューリヒ大学で教授職に就いた。ここで純粋数学の教授をしていたグロスマンと密接に協力しつづけることができるよう、もっと威信がある大学からきた話を蹴ってここを選んだのだ。
アインシュタインは、どのように重力が宇宙を形づくるかについて自分の見方を表現するために新しい数学を必要とし、グロスマンは、その手ほどきをしてやった。だれにとっても同じに見えるように自然法則を「民主的」に書き表わすすべをみつけたいというアインシュタインの願いは、テンソル解析(テンソル計算)と呼ばれる、数学の難解な分野の言葉で書き記すことによって実現できるということを示してやった。テンソル微積分によって、アインシュタインが求める普遍性が保証されるというのだ。また数年前にシュヴァルツシルトが、込み入った曲面の幾何学を探りはじめていたが、グロスマンは、そうした幾何学のついて私たちがもつ理解に起こっていた展開を教えた。それにしてもなぜアインシュタインは、そうしたよじれた幾何学を知らねばならなかったのか。
・
空間が固定されているニュートンの古い見方では、空間という固定された舞台の上でボールがスピンしているのを想像することができる。舞台の上の少し離れたところに立っていれば何の影響も受けない。アインシュタインの見方では事態は大きく違う。空間が、変形するゴムシートのように振舞えば、ボールがスピンすると、まわりの空間がねじれる。いくらか距離をおいて立っていてもその回転と同じ向きに引っ張られる。これは、現実に現れる違いだ。
この世界像を新たな重力理論にするためにアインシュタインがしなければならなかったのは、特別な方程式――重力についての新たな法則を見つけることだった。それは、静止していようが運動していようが何らかのパターンの質量やエネルギーがあると空間の形と、時間の流れる速さがどうなるかを教えてくれるものだった。また、エネルギーのような量が保存されるよう、こうしたパターンがどのように変わることが許されるかを教えてくるものだった。米国の物理学者ジョン・ホイーラーはかってアインシュタインの理論を2つのセンテンスで要約した。「物質は空間に、どのように曲がればよいかを教える。空間は物質に、どう動けばよいかを教える」。
アインシュタインはこうした方程式を、グロスマンから手ほどきを受けたテンソル解析という新しい数学的な言葉で書き表わした。これによって、さまざまな観測者がどのように動いていても――自転しても、加速しても、上下に跳んでも、輪を描いてもこうした方程式は同じように見えることになった。実験室がどのように動いていても観測者は重力について同じ法則を導き出すのだ。
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- -
-
-
-
-
-
-
-
-
-
-
-
-
-
マルセル・グロスマン Google 検索
https://www.google.co.jp/search?q=%E3%83%9E%E3%83%AB%E3%82%BB%E3%83%AB%E3%83%BB%E3%82%B0%E3%83%AD%E3%82%B9%E3%83%9E%E3%83%B3&espv=210&es_sm=93&tbm=isch&tbo=u&source=univ&sa=X&ei=deSrUqO-FMnGlAW-jYHYDA&ved=0CFMQsAQ&biw=941&bih=598